Herleitung: Das ideale Gasgesetz ist die Kombination von drei anderen Gesetzen, die das Verhalten von idealen Gasen beschreiben: Das Boylesche Gesetz (pV = const), das Gesetz von Charles (V:T = const) und das Gesetz von Avogadro (V:n = const) gelten jeweils nur, wenn die im entsprechenden Gesetz nicht erwähnten Größen (zwei aus n, p, T) konstant bleiben.
Das ideale Gasgesetz kombiniert alle drei genannten Beziehungen für beliebige Zustandsänderungen eines idealen Gases und faßt die drei Proportionalitätskonstanten zu einer einzigen, der Gaskonstante R, zusammen (R = 8.31451 JK-1mol-1).
Das ideale Gasgesetz läßt sich auch mit Hilfe der kinetischen Gastheorie herleiten.
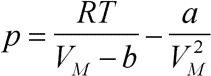
Erläuterung: Die van-der-Waalssche Gleichung ist eine von vielen Näherungen an die wirkliche Zustandsfunktion eines realen Gases. Dabei bleibt sie relativ einfach und anschaulich auf Kosten der Genauigkeit in dem Bereich, in dem eigentlich Verflüssigung des Gases eintritt. Die Gleichung liefert hier sogenannte van-der-Waals-Schleifen, die dem realen Verhalten der Gase nicht entsprechen (z. B. Volumenzunahme bei steigendem Druck).
Herleitung: Man stellt sich vor, daß die Gasteilchen eines realen Gases im gleichen Volumen weniger Raum zur Verfügung haben, als die Teilchen eines idealen Gases. Das ist einsichtig, da die Teilchen eines idealen Gases volumenlos gedacht sind. Wenn b das Eigenvolumen eines Mols Gasteilchen ist, dann reduziert sich das Molvolumen, das den Teilchen für die Bewegung zur Verfügung steht, genau um b. Darum substituiert man das Molvolumen in der idealen Gasgleichung durch VM - b.
Durch die Anziehungskräfte der Teilchen eines realen Gases untereinander verringert sich der Druck der Teilchen auf die Gefäßwand, folglich sinkt der Druck. Es ist klar, daß dieser Effekt umso ausgeprägter ist, je höher die Teilchendichte (n:V bzw. 1:VM2) ist. Darum subtrahiert man a:VM2 vom Druck. Dieser Term wird auch 'Kohäsionsdruck' oder 'innerer Druck' genannt.
Die Zahlenwerte der van-der-Waals-Koeffizienten müssen für jedes Gas experimentell bestimmt werden. Der große Vorteil ist jedoch, daß sie temperaturunabhängig sind.
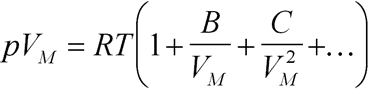
Herleitung: Um die Zustandsgleichung eines realen Gases anzunäheren, nimmt man eine Reihenentwicklung vor.
Das erste Glied der Virialgleichung ist das ideale Gasgesetz. Man verwendet in der Praxis soviele Glieder, wie zur Erreichung der angestrebten Genauigkeit nötig sind (meist genügen die drei angegebenen). Die Zahlenwerte der Virialkoeffizienten B, C usw. müssen experimentell für jedes Gas ermittelt werden und sind zudem temperaturabhängig.