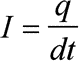
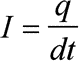
Erläuterung: Der Stromfluß durch einen Leiter ist definiert als Ladungstransport pro Zeit. Ist der Stromfluß hinreichend konstant, dann kann dt direkt durch eine Zeitdifferenz ersetzt werden. Die Stromstärke I besitzt die Einheit Ampere: [I] = 1 Cs-1 = 1 A.
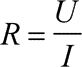
Erläuterung: Es handelt sich hier lediglich um eine Umformung des Ohmschen Gesetzes U = RI. Der elektrische (ohmsche) Widerstand R besitzt die Einheit Ohm: [R] = 1 W.
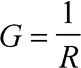
Erläuterung: Die elektrische Leitfähigkeit eines Leiters ist als Kehrwert seines elektrischen Widerstandes definiert. Die Einheit des Leitwertes G ist das Siemens: [G] = 1 W-1 = 1 S.
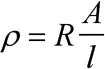
Erläuterung: Der ohmsche Widerstand R ist proportional zur Länge l und umgekehrt proportional zur Fläche A des Leiters. Die Proportionalitätskonstante ist der spezifische Widerstand r, dessen obige Definitionsgleichung man durch Umstellen erhält. Als Einheit ergibt sich Ohm mal Meter: [r] = 1 Wm.
Meistens wird statt des spezifischen Widerstandes die spezifische Leitfähigkeit verwendet.
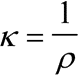
Erläuterung: Die spezifische Leitfähigkeit ist als Kehrwert des spezifischen Widerstandes definiert. Die Einheit ist Siemens pro Meter: [k] = 1 Sm-1.
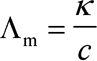
Erläuterung: Man definiert die molare Leitfähigkeit als spezifische Leitfähigkeit pro Mol Stoffmenge, indem man durch die Konzentration c teilt. Als Einheit folgt Siemens pro Meter und Mol: [Lm] = 1 Sm-1mol-1.
Als Referenzwert findet man in der Literatur oft die molare Grenzleitfähigkeit für unendliche Verdünnung L°m. Werte für höhere Konzentrationen starker Elektrolyte erhält man über Kohlrauschs Quadratwurzelgesetz.
Weiterhin definiert man bisweilen noch eine Äquivalentleitfähigkeit
Läq = k:(cz) mit z als Ionenladung.
Erläuterung: Kohlrauschs Quadratwurzelgesetz ist eine empirische Beziehung zur Berechnung von molaren Leitfähigkeiten starker Elektrolyte. Sie berücksichtigt zum einen den Relaxationseffekt der geladenen Teilchen und zum anderen deren elektrophoretische Effekte. In der Stoffkonstante K kommt dennoch in erster Linie nur die Stöchiometrie der Substanz zum Ausdruck.
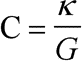
Erläuterung: Bei Leitfähigkeitsmessungen spielt die Beschaffenheit der Meßzelle und besonders die Geometrie der Elektrodenanordnung eine entscheidende Rolle. Deshalb bestimmt man vor einer Messung mit einer bestimmten Meßanordnung deren Zellkonstante C experimentell mit einem Elektrolyten bekannter spezifischer Leitfähigkeit.
Formt man die obige Gleichung nach C = k:G = R:r = l:A um, so wird die geometrische Bedeutung erkennbar. Als Einheit ergeben sich reziproke Zentimeter bzw. Meter.
Für Leitfähigkeitsmessungen bieten sich als Umformungen k = C·G bzw. k = C:R an.